.1)Introduction
Apres avoir présente les différents défauts qui peuvent survenir sur la machine asynchrone dans le premier chapitre, nous allons présenter les méthodes de diagnostic de la machine asynchrone.
D’après certains auteurs [1-4], les méthodes de diagnostic sont classées en deux grandes catégories à savoir :
• Les méthodes de diagnostic sans connaissance a priori ; dite aussi les méthodes sans modèle ou bien externe
• Les méthodes de diagnostic avec connaissance a priori : dite aussi les méthodes de diagnostic avec modèle ou bien interne
Dans un premier temps, nous exposons les méthodes avec modèles ensuite les méthodes sans modèle.
2)Les méthodes de diagnostic avec connaissance a priori
2.1)Principe
Ces méthodes de diagnostic sont généralement employées à partir d'une modélisation physique de la machine. Elles comparent l'évolution du modèle avec celle du processus physique. Considérons la machine asynchrone comme un processus expérimental dont il est question de rechercher, à chaque instant ou période d'échantillonnage, le modèle comportemental correspondant. La (fig. II.1) traduit cette procédure.
2.2)Modèle de la machine asynchrone
2.2.1)Transformation triphasée / biphasée
Les photographies suivantes présentent la machine asynchrone et ses deux principales composantes qui sont le stator et le rotor.
La machine asynchrone est constituée de trois enroulements logés symétriquement dans les encoches du stator et de la cage conductrice intégrée au rotor. Ce dernier est assimilable à trois enroulements identiques parfaitement symétriques et en court-circuit.
On schématise la disposition de ces enroulements (notés a, b, c) sur la (fig.II.4) dans un plan perpendiculaire à l'axe de rotation.
On modélise la machine asynchrone à cage, en fonctionnement sain, dans le repère a, b, c selon les équations en émettant les hypothèses simplificatrices suivantes:
• Le circuit magnétique est linéaire, non saturé, ce qui signifie que les flux sont des fonctions linéaires des courants.
• L'induction dans l'entrefer a une répartition spatiale sinusoïdale.
• La densité surfacique des courants dans les conducteurs est uniforme.
Les équations électriques au stator et au rotor sont alors données par : 2.2.2)Transformation de Park
C'est la transformation des enroulements de phase a, b, c de la machine originelle en des enroulements disposés selon deux axes appelés d et q et équivalents du point de vue électrique et magnétique.
Une matrice unique de transformation est définie pour les courants, les tensions et les flux :
θ est l'angle électrique entre le stator et l'axe d. L'indice (0) désigne les composantes homopolaires (ces composantes sont égales à zéro dans le cas d'un système triphasé équilibré).
Si θ est nul alors on obtient la matrice [C], appelée matrice de Concordia telle que :
2.3)Le diagnostic par l’estimation paramétriqueCette méthode de diagnostic utilise les paramètres structuraux d'un modèle de connaissance, et extrait par la suite les paramètres du système à partir des lois de connaissance pour détecter et localiser les défaillances. Le point essentiel dans l'efficacité de cette méthode est le choix du modèle de connaissance. En effet, le type de défaut quel'on voudra détecter sera fonction du modèle utilisé.
Les premiers travaux relatant de l'estimation de paramètres ont débuté avec des modèles relativement simples (modèle de Park par exemple) utilisés depuis plusieurs années pour la commande des machines électriques. Ces modèles n'ont besoin que de quatre paramètres pour effectuer le diagnostic de défaut ce qui, dans certain cas, ne permet pas de localiser avec précision la défaillance. L'étape suivante est donc nécessairement le passage à un modèle de connaissance plus fin de la machine, tout en gardant la possibilité d'identifier les paramètres souhaités. Ces modèles peuvent être des modèles triphasés, qui s'affranchissent de l'hypothèse d'une machine magnétiquement équilibrée, ou encore des modèles à n phases, capables de refléter le fonctionnement de la machine sur une large bande de fréquences.
Des algorithmes spécifiques ont été élaborés pour l'estimation séquentielle de paramètres.
Le filtre de Kalman apparaît comme le plus adéquat de tous mais aussi le plus délicat à mettre en oeuvre. Tout d'abord, en tant qu'algorithme d'identification en temps réel, le filtre de Kalman étendu délivre un modèle adaptatif, capable de prendre en compte les évolutions normales des paramètres de la machine telles que la variation des résistances (en fonction de la température) ou encore la variation des inductances (en fonction du niveau de saturation). Par ailleurs, les paramètres estimés, eux-mêmes, permettent une première analyse des conditions de fonctionnement de la machine. Par exemple, une augmentation anormale de la valeur des résistances statoriques peut signifier un échauffement excessif et donc une dégradation progressive des enroulements, [10].
2.4)Le diagnostic par les techniques d'identification
L'identification est la détermination, à partir de la connaissance des signaux d'entrées et de sorties, d'un modèle mathématique appartenant à une classe donnée pour lequel les comportements dynamiques ou statiques sont équivalents à ceux du processus au sens d'un critère donné.
Donc, le processus de diagnostic peut se faire selon les étapes suivantes:
Le choix d'un modèle mathématique
Le choix des signaux d'entrées et de sorties
Un critère de similitude entre le modèle et le processus
Le processus d'identification [Ljung 87] se base par la suite sur un algorithme d'optimisation de l'erreur entre les paramètres du modèle et ceux du système étudié. [Khelif 94] présente l'application de quelques algorithmes pour l'identification des paramètres de la machine asynchrone.
Ces méthodes ne sont pas utilisables en temps réel puisqu'il est nécessaire de connaître à l'avance les enregistrements des signaux d'entrées et de sorties, [1].
S (t) m correspond à la sortie du processus S (t) P , alors le modèle fournit une estimation des grandeurs caractéristiques du fonctionnement sans défaut. La détection de défaillance est réalisée par le suivi de l'erreur de sortie ε (t) (méthode des résidus) ou par la mise en évidence d'un écart entre le modèle (qui s'éloigne alors de la physique du phénomène) et le processus réel.
Dans le second cas, l'erreur de sortie peut être minimisée en modifiant les paramètres structuraux du modèle. De cette manière les paramètres inhérents au système sont identifiés et suivis même en cas de défaillance. Le modèle adapté donne alors une signature du mode de fonctionnement, [4].
Apres avoir présente les différents défauts qui peuvent survenir sur la machine asynchrone dans le premier chapitre, nous allons présenter les méthodes de diagnostic de la machine asynchrone.
D’après certains auteurs [1-4], les méthodes de diagnostic sont classées en deux grandes catégories à savoir :
• Les méthodes de diagnostic sans connaissance a priori ; dite aussi les méthodes sans modèle ou bien externe
• Les méthodes de diagnostic avec connaissance a priori : dite aussi les méthodes de diagnostic avec modèle ou bien interne
Dans un premier temps, nous exposons les méthodes avec modèles ensuite les méthodes sans modèle.
2)Les méthodes de diagnostic avec connaissance a priori
2.1)Principe
Ces méthodes de diagnostic sont généralement employées à partir d'une modélisation physique de la machine. Elles comparent l'évolution du modèle avec celle du processus physique. Considérons la machine asynchrone comme un processus expérimental dont il est question de rechercher, à chaque instant ou période d'échantillonnage, le modèle comportemental correspondant. La (fig. II.1) traduit cette procédure.
Partant d'un modèle du processus à surveiller sain. Si la sortie du modèle
2.2.1)Transformation triphasée / biphasée
Les photographies suivantes présentent la machine asynchrone et ses deux principales composantes qui sont le stator et le rotor.
La machine asynchrone est constituée de trois enroulements logés symétriquement dans les encoches du stator et de la cage conductrice intégrée au rotor. Ce dernier est assimilable à trois enroulements identiques parfaitement symétriques et en court-circuit.
On schématise la disposition de ces enroulements (notés a, b, c) sur la (fig.II.4) dans un plan perpendiculaire à l'axe de rotation.
On modélise la machine asynchrone à cage, en fonctionnement sain, dans le repère a, b, c selon les équations en émettant les hypothèses simplificatrices suivantes:
• Le circuit magnétique est linéaire, non saturé, ce qui signifie que les flux sont des fonctions linéaires des courants.
• L'induction dans l'entrefer a une répartition spatiale sinusoïdale.
• La densité surfacique des courants dans les conducteurs est uniforme.
Les équations électriques au stator et au rotor sont alors données par : 2.2.2)Transformation de Park
C'est la transformation des enroulements de phase a, b, c de la machine originelle en des enroulements disposés selon deux axes appelés d et q et équivalents du point de vue électrique et magnétique.
Une matrice unique de transformation est définie pour les courants, les tensions et les flux :
θ est l'angle électrique entre le stator et l'axe d. L'indice (0) désigne les composantes homopolaires (ces composantes sont égales à zéro dans le cas d'un système triphasé équilibré).
Si θ est nul alors on obtient la matrice [C], appelée matrice de Concordia telle que :
2.3)Le diagnostic par l’estimation paramétriqueCette méthode de diagnostic utilise les paramètres structuraux d'un modèle de connaissance, et extrait par la suite les paramètres du système à partir des lois de connaissance pour détecter et localiser les défaillances. Le point essentiel dans l'efficacité de cette méthode est le choix du modèle de connaissance. En effet, le type de défaut quel'on voudra détecter sera fonction du modèle utilisé.
Les premiers travaux relatant de l'estimation de paramètres ont débuté avec des modèles relativement simples (modèle de Park par exemple) utilisés depuis plusieurs années pour la commande des machines électriques. Ces modèles n'ont besoin que de quatre paramètres pour effectuer le diagnostic de défaut ce qui, dans certain cas, ne permet pas de localiser avec précision la défaillance. L'étape suivante est donc nécessairement le passage à un modèle de connaissance plus fin de la machine, tout en gardant la possibilité d'identifier les paramètres souhaités. Ces modèles peuvent être des modèles triphasés, qui s'affranchissent de l'hypothèse d'une machine magnétiquement équilibrée, ou encore des modèles à n phases, capables de refléter le fonctionnement de la machine sur une large bande de fréquences.
Des algorithmes spécifiques ont été élaborés pour l'estimation séquentielle de paramètres.
Le filtre de Kalman apparaît comme le plus adéquat de tous mais aussi le plus délicat à mettre en oeuvre. Tout d'abord, en tant qu'algorithme d'identification en temps réel, le filtre de Kalman étendu délivre un modèle adaptatif, capable de prendre en compte les évolutions normales des paramètres de la machine telles que la variation des résistances (en fonction de la température) ou encore la variation des inductances (en fonction du niveau de saturation). Par ailleurs, les paramètres estimés, eux-mêmes, permettent une première analyse des conditions de fonctionnement de la machine. Par exemple, une augmentation anormale de la valeur des résistances statoriques peut signifier un échauffement excessif et donc une dégradation progressive des enroulements, [10].
2.4)Le diagnostic par les techniques d'identification
L'identification est la détermination, à partir de la connaissance des signaux d'entrées et de sorties, d'un modèle mathématique appartenant à une classe donnée pour lequel les comportements dynamiques ou statiques sont équivalents à ceux du processus au sens d'un critère donné.
Donc, le processus de diagnostic peut se faire selon les étapes suivantes:
Le choix d'un modèle mathématique
Le choix des signaux d'entrées et de sorties
Un critère de similitude entre le modèle et le processus
Le processus d'identification [Ljung 87] se base par la suite sur un algorithme d'optimisation de l'erreur entre les paramètres du modèle et ceux du système étudié. [Khelif 94] présente l'application de quelques algorithmes pour l'identification des paramètres de la machine asynchrone.
Ces méthodes ne sont pas utilisables en temps réel puisqu'il est nécessaire de connaître à l'avance les enregistrements des signaux d'entrées et de sorties, [1].
S (t) m correspond à la sortie du processus S (t) P , alors le modèle fournit une estimation des grandeurs caractéristiques du fonctionnement sans défaut. La détection de défaillance est réalisée par le suivi de l'erreur de sortie ε (t) (méthode des résidus) ou par la mise en évidence d'un écart entre le modèle (qui s'éloigne alors de la physique du phénomène) et le processus réel.
Dans le second cas, l'erreur de sortie peut être minimisée en modifiant les paramètres structuraux du modèle. De cette manière les paramètres inhérents au système sont identifiés et suivis même en cas de défaillance. Le modèle adapté donne alors une signature du mode de fonctionnement, [4].





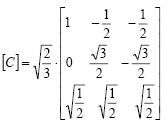
Aucun commentaire:
Enregistrer un commentaire